This post illustrates the circuit design of Sequence Detector for the pattern “1101”. State Machine diagram for the same Sequence Detector has been shown below. Click here to realize how we reach to the following state transition diagram.
Click here to learn the step by step procedure of “How to synthesize a state machine / How to boil down a state machine to the circuit level”.
Now as we have the state machine with us, the next step is to encode the states. For 4 states:
State Encoding
S0 00
S1 01
S2 10
S3 11
We need only 2 flipflops to represent these 4 states. For this example we will be using T Flipflips to design the circuit.
Let’s draw the state transition table using the Excitation table of T flipflop
| PS
Q2(t) Q1(t) | X
Input | NS
Q2(t+1) Q1(t+1) | Excite (T)
T2 T1 | O
Output |
| 0 0 | 0 | 0 0 | 0 0 | 0 |
| 0 0 | 1 | 0 1 | 0 1 | 0 |
| 0 1 | 0 | 1 0 | 1 1 | 0 |
| 0 1 | 1 | 0 1 | 0 0 | 0 |
| 1 0 | 0 | 0 0 | 1 0 | 0 |
| 1 0 | 1 | 1 1 | 0 1 | 0 |
| 1 1 | 0 | 1 0 | 0 1 | 0 |
| 1 1 | 1 | 0 1 | 1 0 | 1 |
Now to realize the combinational logic we have to find out the Boolean expression for 3 output variables (of the above table) T2, T1 and O in terms of 3 input variable Q2(t), Q1(t) and X.
| T2 | T1 |
 |  |
| Y | Boolean Expressions |
 | T2 = Q2′(t)Q1(t)X’ + Q2(t)Q1′(t)X’ +
Q2(t)Q1(t)X T1 = Q1(t)X’ + Q1′(t)X = Q1(t) ⊕ X O = Q2(t)Q1(t)X |
Let’s draw the respective circuit diagram for the given Sequence Detector.
can you please explain the asynchronous sequence detector or any finite state machine
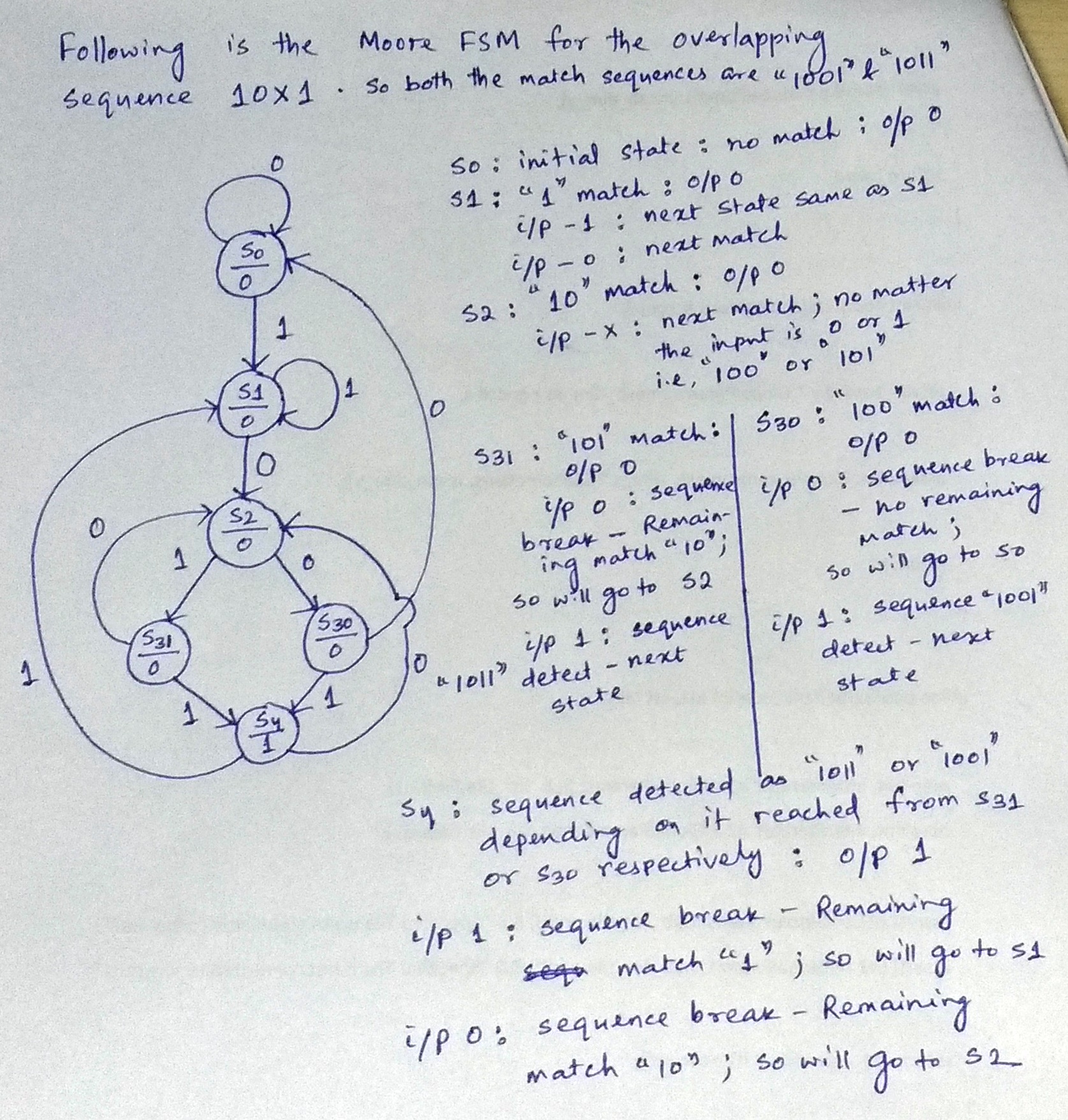
can you please draw moore FSM overlapping for 10X1 sequence detection
Dear Babu,
Sorry for replying you so late. Hope you must have resolved the problem. But for your reference and for the reference of the other readers we are posting the solution of your query. In the following figure I have drawn the FSM with the detection of bit from MSB towards LSB, whereas in the above published post the detection is done from LSB to MSB.
